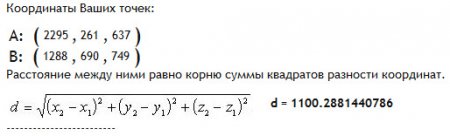В данной статье мы подробно рассмотрели основные принципы работы с датакартами, условные обозначения на них. Вы узнаете как правильно читать карты от стапельной системы Кар-О-лайнер, вычислять линейные размеры кузова используя контрольные точки в трехмерной системе координат XYZ.
К сожалению, у многих мастеров кузовного ремонта возникают трудности с пониманием и использованием датакарт от стапельных систем car-o-liner, autorobot. Больше всего проблем связано с трехмерной системой координат, а точнее с пониманием проекционной длины в указанных схемах.
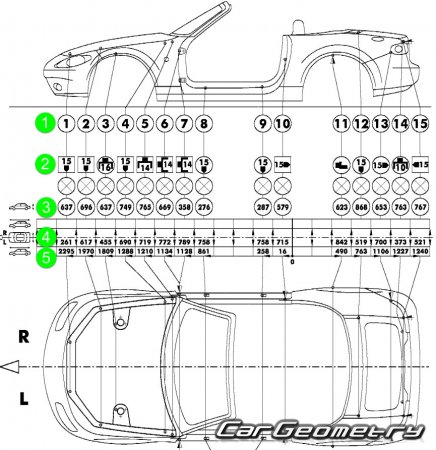
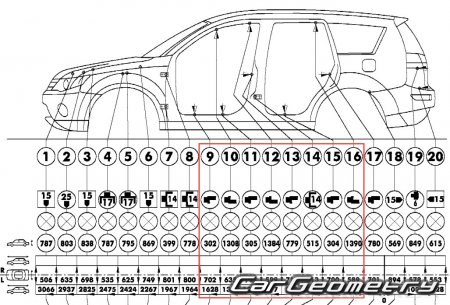
Давайте посмотрим на пример стандартной карты данных от стапельной системы
1) Номер контрольной точки
2) Вид и размер используемой головки
3) Высота
4) Ширина (если кузов не симметричен указывается два отдельных значения для L и R)
5) Длина (Проекционная )
Линейные размеры кузова – это расстояние между двумя точками (расположенными на одной высоте), которые можно измерять с помощью обычной рулеткой, механической или электронной линейкой.
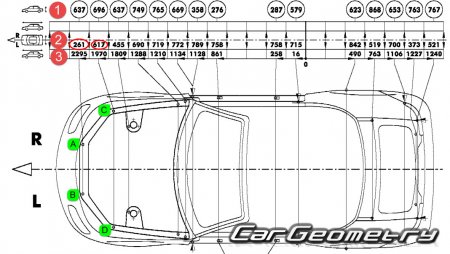
1) ВЫСОТА контрольной точки
2) ШИРИНА (линейная). Если цифра расположена в нижней графе (в нашем случае 261), то кузов симметричен и расстояние между точками AB = 261*2 = 522 mm . Аналогично для CD=617*2= 1234 mm.
3) ДЛИНА (проекционная) . Обратите внимание на то, что данное значение является ПРОЕКЦИОННЫМ. В задней части кузова (в районе задних сидений) производители стапеля назначают нулевую точку (на нашей схеме она обозначается 0) и ведут измерения по длине кузова по направлению к переднему и заднему бамперу.
В стапельных системах «Линейными размерами» можно считать данные по ширине кузова. Большинство кузовов являются симметричными, поэтому производители стапелей приводят эти данные от оси симметрии (делят на ДВА).
В нашем случае для вычисления расстояния между точками AB мы умножали 261*2.
Если кузов автомобиля является не симметричным, то в датакарте указывается два значения по ширине для ЛЕВОЙ «L» и ПРАВОЙ «R» стороны отдельно. В данном случае кузов является симметричным и в графе 2 указаны данные только для левой стороны (261).
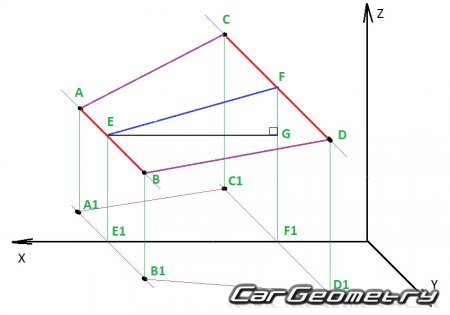
Для того, что бы разобраться, что такое Проекционная ДЛИНА нарисуем трехмерный схематический рисунок наших точек A-B-C-D в трехмерной системе координат, где Х –длина, Y- ширина, Z – высота.
Допустим нам нужно высчитать линейное расстояние между точками AC.
Если мы внимательно посмотрим на нашу датакарту, то увидим, что точка A и B имею т высоту 637 мм, а точка С и D 696 мм от плоскости расположения нулевой точки кузова по оси Z.
Обратите внимание, что линия EF это воображаемая ось симметрии, которая делит кузов пополам.
Значения ДЛИНЫ указанные в датакарте (2295 и 1970) это проекции точек EF на плоскость XY или удаления точек E1 и F1 от нулевой точки по оси X. Следовательно, мы легко можем посчитать значение E1-F1=2295-1970= 325 мм
ВНИМАНИЕ: Многие мастера путают значения «проекционной длины» и считают, что EF=E1F1. Если точки E и F (A и C) расположены на разной высоте, то НИКОГДА EF не будет равно E1F1
Давайте вычислим значение EF используя теорему Пифагора:
Мы знаем, что E-E1 = F1-G = 637 мм, F-F1= 696 мм, а E1-F1=EG=2295-1970= 325 мм
Вычисляем значение FG = FF1 – EE1 = 696-637 = 59 mm
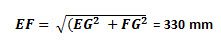
Чем больше разница по высоте между двумя исходными точками, тем значительнее будет различаться значения EF и E1F1.
Теперь зная значение EF мы аналогичным способом (Теорема Пифагора) можем посчитать линейное расстояние AC. EF= 330 мм. CF-AE=617-261= 356 мм
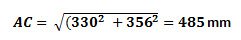
Понимая, что значения в датакарте указаны в трехмерной системе координат (Х –длина, Y- ширина, Z – высота) и используя онлайн калькуляторы мы легко можем посчитать практически любые линейные размеры между двумя любыми точками.
Теперь представим, что нам нужно посчитать линейную диагональ между точками AD
Значения точки A мы берем напрямую с датакарты A: (2295 , 261 , 637)
Точка D симметрична С и имеет то же значение по длины X и высотe Z, но ширина у D примет отрицательное значение -617 (удалена от оси симметрии на то же значение, но в противоположную сторону). Получаем D: (1970 , -617 , 696)
Вернемся к нашей датакарте и просчитаем несколько примеров:
Расчёт линейного размера между точками 1 и 4 (на одной стороне):
Расчёт линейного размера между точками 2 и 4 (по диагонали):
Главное, запомнить, что для вычисления диагонали между двумя точками значение второй точки по ширине (оси Y) нужно указывать с отрицательным значением.
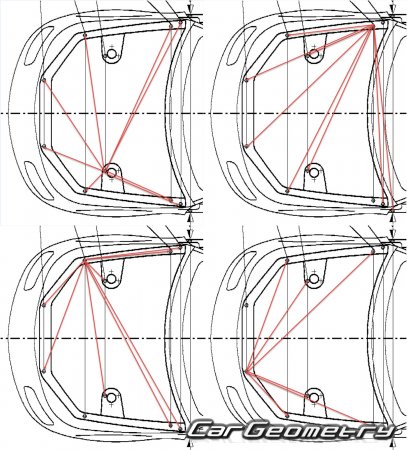
В итоге, имея координаты всего 5 точек в передней части мы легко можем высчитать более 30 различных линейных размеров. Ниже приведены только некоторые примеры:
Аналогичным образом можно вычислять линейные размеры проемов дверей:
Нас интересуют координаты точек 9-16. Рассчитаем расстояние между 9-12:
Или например 15-16:
И пример размеров дверных проемов, которые можно легко вычислить используя представленную выше датакарту:
В общем при наличии минимального количества времени и желания можно посчитать большинство "необходимых" для ремонта линейных размеров кузова.
Главное не забывать, что при измерении оригинальными линейками могут использоваться дополнительные насадки, тип и размер которых также указан в каждой датакарте.
Мы надеемся что приведенная в данной статье информация будет полезна как специалистам кузовного ремонта, так и любителям, которые только осваивают работу с измерительными линейками car-o-liner или autorobot, поможет избежать ошибок при измерениях кузова и существенно уменьшить время восстановления геометрии кузова по контрольным точкам.